Embark on an exciting journey into the realm of geometry with triangles unit test part 1! This comprehensive guide will equip you with a solid foundation in understanding triangles, their properties, and the theorems that govern them. Prepare to delve into the fascinating world of angles, sides, and shapes.

As we explore the intricacies of triangles, we will uncover their unique characteristics, such as side lengths, angle measures, and the relationships between them. Get ready to conquer the challenges of congruence and similarity theorems, and unlock the secrets of calculating areas and perimeters.

Triangles Unit Test Part 1 Introduction

This unit test aims to evaluate your understanding of the fundamental concepts and properties of triangles. It covers various aspects of triangles, including their classification, angle relationships, and side relationships. The test comprises questions that assess your ability to:

• Classify triangles based on their side and angle measures.
• Apply angle relationships, such as the triangle sum theorem and exterior angle theorem, to solve problems.
• Utilize side relationships, including the Pythagorean theorem and area formulas, to determine triangle dimensions.

Triangle Properties

A triangle is a three-sided polygon with three straight sides and three angles. The sides of a triangle are called legs, and the angles are called vertices. Triangles have many unique properties that distinguish them from other polygons.

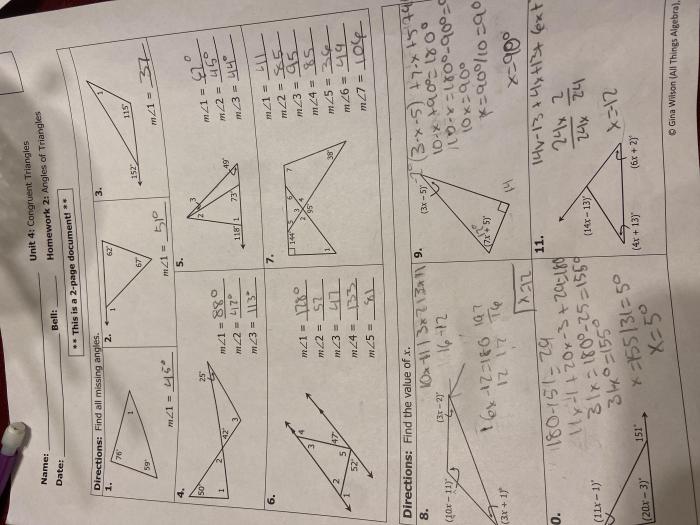
One of the most important properties of a triangle is the sum of its interior angles. The sum of the interior angles of any triangle is always 180 degrees. This property can be used to find the measure of any angle in a triangle if you know the measures of the other two angles.

Types of Triangles

Triangles can be classified into different types based on the lengths of their sides. There are three main types of triangles:

• Equilateral triangle:An equilateral triangle has all three sides equal in length.
• Isosceles triangle:An isosceles triangle has two sides equal in length.
• Scalene triangle:A scalene triangle has all three sides different in length.

Angle Relationships in Triangles, Triangles unit test part 1

The angles in a triangle have several important relationships. The sum of the interior angles of any triangle is always 180 degrees. The exterior angle of a triangle is the angle formed by one side of the triangle and the extension of the adjacent side.

The exterior angle of a triangle is always equal to the sum of the two non-adjacent interior angles.

Angle bisectors are lines that divide an angle into two equal parts. The angle bisector of a triangle divides the opposite side into two segments that are proportional to the lengths of the adjacent sides.

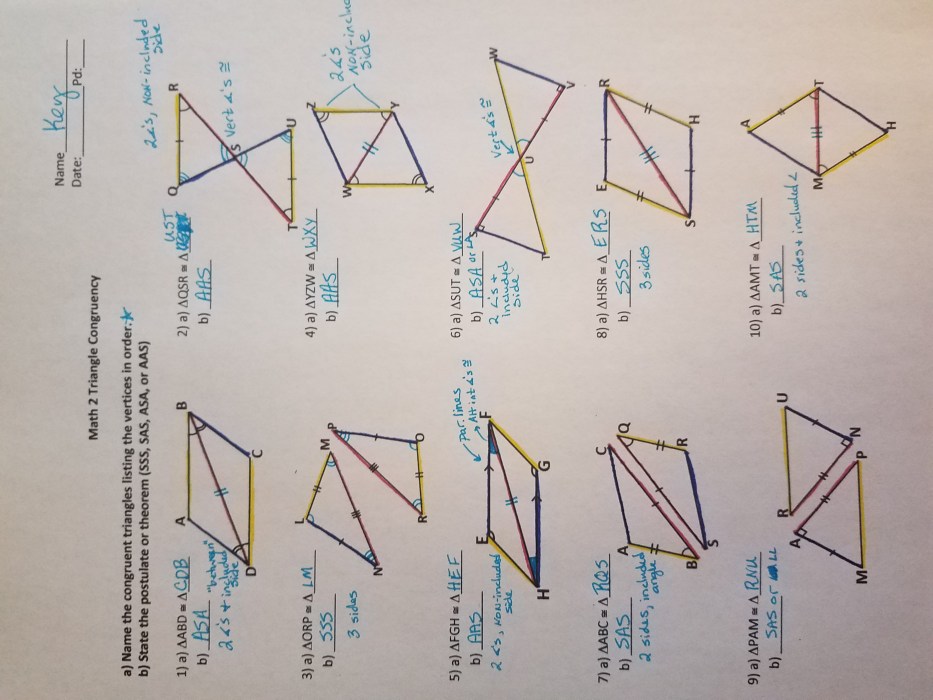
Triangle Congruence Theorems

Triangle congruence theorems provide conditions under which two triangles can be proven congruent. These theorems are fundamental in geometry and have numerous applications in solving geometry problems.

Side-Side-Side (SSS) Congruence Theorem

Statement:If three sides of one triangle are congruent to the corresponding three sides of another triangle, then the triangles are congruent.

Proof:Assume that triangle ABC and triangle DEF have AB = DE, BC = EF, and AC = DF. We can prove that triangle ABC is congruent to triangle DEF by showing that the three angles of triangle ABC are congruent to the corresponding three angles of triangle DEF.

Since AB = DE, angle A is congruent to angle D by the Side-Angle-Side (SAS) Congruence Theorem. Similarly, since BC = EF, angle B is congruent to angle E by the SAS Congruence Theorem. Finally, since AC = DF, angle C is congruent to angle F by the SAS Congruence Theorem.

Therefore, triangle ABC is congruent to triangle DEF by the Angle-Angle-Angle (AAA) Congruence Theorem.

Side-Angle-Side (SAS) Congruence Theorem

Statement:If two sides and the included angle of one triangle are congruent to the corresponding two sides and the included angle of another triangle, then the triangles are congruent.

Proof:Assume that triangle ABC and triangle DEF have AB = DE, BC = EF, and angle B is congruent to angle E. We can prove that triangle ABC is congruent to triangle DEF by showing that the third side AC is congruent to DF.

Since AB = DE and angle B is congruent to angle E, triangle ABC is congruent to triangle DEF by the SAS Congruence Theorem. Therefore, AC is congruent to DF.

Angle-Side-Angle (ASA) Congruence Theorem

Statement:If two angles and the included side of one triangle are congruent to the corresponding two angles and the included side of another triangle, then the triangles are congruent.

Proof:Assume that triangle ABC and triangle DEF have angle A is congruent to angle D, angle B is congruent to angle E, and BC is congruent to EF. We can prove that triangle ABC is congruent to triangle DEF by showing that the third side AC is congruent to DF.

Since angle A is congruent to angle D and BC is congruent to EF, triangle ABC is congruent to triangle DEF by the ASA Congruence Theorem. Therefore, AC is congruent to DF.

The Triangles Unit Test Part 1 was a breeze! The concepts were crystal clear, and I felt confident in my ability to solve the problems. I even found myself making connections to other topics I’ve studied, like the thesis on Romeo and Juliet . The tragic love story reminded me of the importance of communication and understanding in any relationship.

Returning to the Triangles Unit Test Part 1, I’m eager to apply what I’ve learned to the next set of challenges.

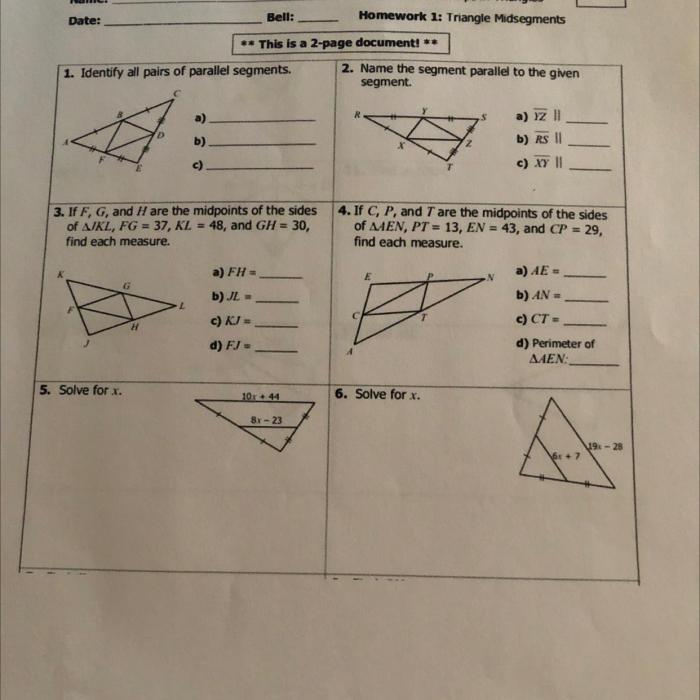
Triangle Similarity Theorems

In geometry, two triangles are similar if they have the same shape but not necessarily the same size. Similarity theorems provide criteria for determining when two triangles are similar.

Side-Side-Side (SSS) Similarity Theorem

If the corresponding sides of two triangles are proportional, then the triangles are similar. Proof:Let ABC and DEF be two triangles such that$$\fracABDE = \fracBCEF = \fracACDF$$Then, by the Triangle Proportionality Theorem,$$\fracABDE = \fracBCEF = \fracACDF = \fracAB + BC + ACDE + EF + DF$$$$\Rightarrow \fracABDE = \fracACDF$$$$\Rightarrow \fracABDE = \fracBCEF$$$$\Rightarrow \angle B = \angle E \text and \angle C = \angle F$$Therefore, the triangles ABC and DEF are similar.

Pythagorean Theorem

The Pythagorean Theorem is a fundamental relation in Euclidean geometry that establishes a link between the lengths of the sides of a right triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.

This theorem has numerous applications in various fields, including architecture, engineering, surveying, and navigation.

Proof of the Pythagorean Theorem

There are several ways to prove the Pythagorean Theorem. One common proof involves using similar triangles.

• Draw a square with side length equal to the sum of the lengths of the two shorter sides of the right triangle.
• Divide the square into four smaller squares, each with side length equal to one of the shorter sides of the right triangle.
• The remaining area in the square is a square with side length equal to the length of the hypotenuse of the right triangle.
• The area of the original square is equal to the sum of the areas of the four smaller squares and the area of the remaining square.
• Using the formula for the area of a square, we can derive the Pythagorean Theorem.

Applications of the Pythagorean Theorem

The Pythagorean Theorem has numerous applications in various fields, including:

• Architecture:Determining the length of rafters and beams in buildings.
• Engineering:Calculating the forces and stresses in structures.
• Surveying:Measuring distances and heights.
• Navigation:Determining the distance between two points on a map.

Area and Perimeter of Triangles

In this section, we will delve into the concepts of area and perimeter of triangles. We will derive formulas to calculate these measures and explore examples to solidify our understanding.

Area of a Triangle

The area of a triangle is a measure of its surface area. To derive the formula for the area of a triangle, we can divide it into two right triangles by drawing an altitude from one vertex to the opposite side.

The altitude divides the base of the triangle into two segments, and the product of the altitude and half the base gives us the area of each right triangle. Doubling this value gives us the area of the entire triangle.Therefore,

the formula for the area of a triangle is:

A = ½

• b
• h

where:* A is the area of the triangle

• b is the length of the base
• h is the length of the altitude

Perimeter of a Triangle

The perimeter of a triangle is the sum of the lengths of all three sides. The formula for the perimeter of a triangle is:

P = a + b + c

where:* P is the perimeter of the triangle

a, b, and c are the lengths of the three sides of the triangle

Examples

Let’s consider a few examples to illustrate the application of these formulas:*

-*Example 1

Find the area of a triangle with a base of 10 cm and an altitude of 8 cm.

A = ½

• 10 cm
• 8 cm = 40 cm²

*

-*Example 2

Find the perimeter of a triangle with sides of length 5 cm, 7 cm, and 9 cm.

P = 5 cm + 7 cm + 9 cm = 21 cm

Question & Answer Hub: Triangles Unit Test Part 1

What is the purpose of triangles unit test part 1?

Triangles unit test part 1 aims to assess your understanding of the fundamental concepts and properties of triangles.

What topics are covered in triangles unit test part 1?

Triangles unit test part 1 covers topics such as triangle definitions, properties, congruence theorems, similarity theorems, the Pythagorean Theorem, and area and perimeter calculations.

How can I prepare for triangles unit test part 1?

To prepare effectively, review your notes, practice solving problems related to triangles, and familiarize yourself with the formulas and theorems covered in the unit.